LDPC codes
Encoder and message passing decoder for LDPC codes (802.11n)
Introduction
Low density parity check (LDPC) codes are linear block codes approaching capacity. Turbo codes are an example of another capacity-approacing code family. There are many applications that use LDPC codes, including the standard for the satellite transmission DVB-S2, 10GBase-T Ethernet, and 802.11 Wi-Fi standard. LDPC codes are defined by a sparse parity check matrix that determines the performance of the transmission. The maximum likelihood decoding of an LDPC code is an NP-complete problem and sub-optimal decoding techniques rely on belief propagation.
This project cosinsts in the implementation in MATLAB of the encoder and message passing decoder for the LDPC codes used in the IEEE 802.11n standard. After a brief description of the encoder and fields of applications, the sum-product algorithm for message passing decoder is presented. The performance are then evaluated in AWGN settings in terms of BER and PER.
Implementation
The encoder uses a parity check matrix H of size 324x648, i.e. R = 1/2. The matrix is made of 27x27 blocks obtained by circular shifts of the prototype matrix
and blocks of zeros. In order to generate valid codes the matrix H needs to be inverted. Exploiting its particular properties, H can be decomposed in 6 blocks and codes can be generated in linear time instead of cubic.
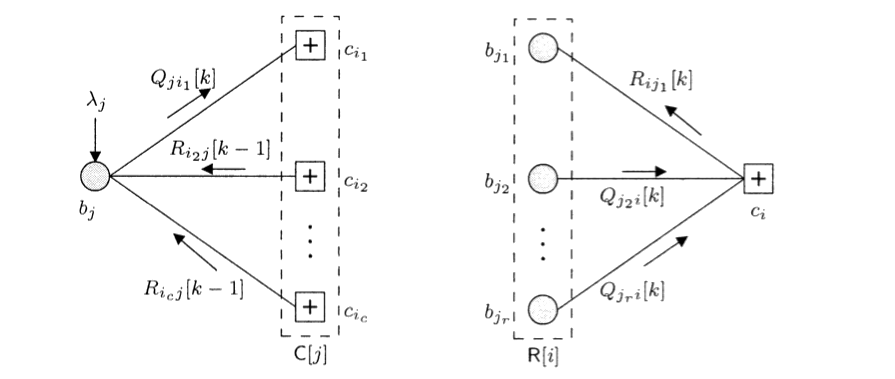
The decoder is implemented using the sum-product algorithm in the log domain so that products become sums. Messages are exchanged in an iterative way between variable nodes, representing the columns of H, and check nodes, representing the rows of H.